コンプレックス (複雑な) サンプルの統計データを分析
正確な調査結果を解釈
IBM SPSS Complex Samples で調査分析にサンプル設計を組み込むことにより、市場や世論の調査担当者や社会科学者は、統計的により有効な推定を行えるようになります。 SPSS Complex Samples では、コンプレックス・サンプル設計に取り組む際に必要な、層化抽出法、クラスター化抽出法、複数段階抽出法などの専門的な計画ツールや統計手法を使用できます。
- サンプル設計を調査分析に組み込むことで、より正確な結果を導きます。
- 調査計画パラメーターを再利用できるように保持し、分析の迅速化と効率の向上を図ります。
- 徹底的かつ詳細な分析を行うために、複雑な調査データを管理します。
- 直感的なインターフェースと便利なウィザードの使用により、データの分析と調査結果の解釈を迅速化します。
SPSS Complex Samples詳細情報
分析へのサンプル設計の組み込み
- サンプルの精度を高めたり、代表サンプルが主要グループから抽出されるようにします。
- サンプル抽出単位のクラスターまたはグループを選択することで、調査の費用対効果を高めます。
- 他段階抽出法を使用して、より高次のサンプルを選択します。
再利用のために調査計画パラメーターを保持
- 実施した抽出および分析計画を含むデータ・セットを一般利用のために公開できます。
- 公開された計画は、テンプレートとして使用でき、そこに計画作成時の意思決定を保存できます。
- 組織内の他のユーザーが計画を使用できるようにすることで、誰もが結果を再現したり、途中から作業を引き継いだりできるようになります。
複雑な調査データの管理
- 1 次元の度数表または二次元のクロス集計表とそれに関連する標準誤差、設計効果、信頼区間、および仮説検定を表示します。
- 線形回帰、分散分析 (ANOVA)、および共分散分析 (ANCOVA) モデルを構築します。
- コンプレックス・サンプル抽出手法によって抽出されたサンプルの、平均/合計/比率を推定し、標準誤差、設計効果、信頼区間、および仮説検定を計算します。
- 2 項ロジスティック回帰分析と多項ロジスティック回帰 (MLR) 分析を実行します。
- Cox 比例ハザード回帰を生存時間分析に適用します。
直感的なインターフェースと便利なウィザードの使用
- 分析準備ウィザードを使用してサンプルの定義方法と標準誤差の推定方法を指定します。
- 自分でサンプルを作成する場合は、サンプル抽出計画ウィザードを使用して枠組みを定義し、サンプルを抽出します。
- IBM SPSS Complex Samples Selection (CSSELECT) プロシージャーを使用すると、母集団から確率に基づいてコンプレックス・サンプルを抽出し、同時に特定のサブグループの代表が過少または過多にならないようにできます。
SPSS Complex Samplesの画面イメージ
ランディング・ページ
サンプル・データを分析するために、Complex Sample Descriptives や Complex Sample Tabulate の入力として、分析計画ウィザードで作成した分析設計を使用できます。
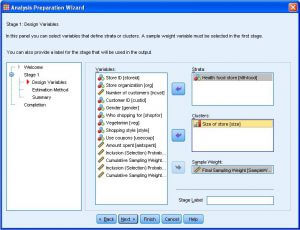
一般線形モデル
分散モデルの線形回帰と分析を作成することによって、サンプル設計を考慮に入れながら数値結果を予測できます。このプロシージャーでは、サンプルの選択に使用したサンプル設計 (等確率と PPS の方式、WR と WOR のサンプル抽出プロシージャーなど) を考慮に入れながら、分散状況を推定します。
パラメーター推定値
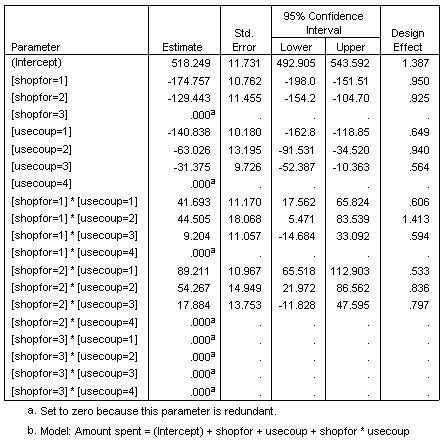
このパラメーター推定値によって、支払い額に対する各予因子の効果を確認できます。切片項の 518.249 という値が示しているとおり、この食料品店チェーンでは、新聞やターゲット・メールのクーポンを利用する家族連れの買い物客が平均で 518.25 ドルを支払うということを予測できます。
パラメーター推定値は、モデルの各項の効果を定量化するために便利ですが、推定限界平均値の表を使用すれば、さらに簡単にモデルの結果を解釈できるようになります。
サンプリング計画ウィザード
サンプリングのフレームを指定して、Complex Samples のアドオン・モジュールにあるコンパニオン・プロシージャーで使用する複合的なサンプル設計を作成できます。
サンプルを抽出する場合は、Complex Sample Selection プロシージャーの入力として、サンプリング計画ウィザードで作成したサンプル設計を使用します。